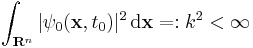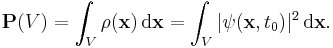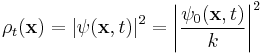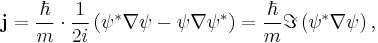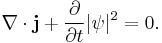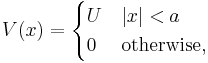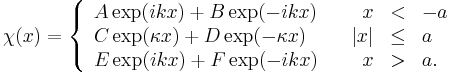Probability amplitude

In quantum mechanics, a probability amplitude is a complex number whose absolute value squared represents a probability or probability density. For example, the values taken by a normalised wave function $ψ$ are amplitudes, since $| ψ (x)| 2$ gives the probability density at position $x$ . Probability amplitudes may also correspond to probabilities of discrete outcomes.

The principal use of probability amplitudes is as the physical meaning of the wavefunction, a link first proposed by Max Born and a pillar of the Copenhagen interpretation of quantum mechanics. In fact, the properties of the wave function were being used to make physical predictions (such as emissions from atoms being at certain discrete energies) before any physical interpretation was offered. Born was awarded half of the 1954 Nobel Prize in physics for this understanding, though it was vigorously contested at the time by the original physicists working on the theory, such as Schrödinger and Einstein. Therefore, the probability thus calculated is sometimes called the "Born probability", and the relationship used to calculate probability from the wavefunction is sometimes called the Born rule.

These probability amplitudes have special significance because they act in quantum mechanics as the equivalent of conventional probabilities, with many analogous laws. For example, in the classic double-slit experiment where electrons are fired randomly at two slits, an intuitive interpretation is that $P (hit either slit) = P (hit first slit) + P (hit second slit)$ , where $P (event)$ is the probability of that event. However, it is impossible to observe which slit is passed through without altering the electron. Thus, when not watching the electron, the particle cannot be said to go through either slit and this simplistic explanation does not work. However, the complex amplitudes taken by the two wavefunctions which represent the electron passing each slit do follow a law of precisely the form expected ( $ψ total = ψ first + ψ second$ ), and the calculations agree with experiment. This is the principle of quantum superposition, and explains the requirement that amplitudes be complex, as a purely real formulation has too few dimensions to describe the system's state when superposition is taken into account.^[1]

1 Wavefunctions as amplitudes
2 Discrete amplitudes
- 2.1 Example: One-dimensional quantum tunnelling
3 Notes

Wavefunctions as amplitudes

Normalisable states

The Schrödinger wave equation, describing states of quantum particles, has solutions that describe a system and determine precisely how the state changes with time. Suppose a state $ψ 0 (x, t)$ is a solution of the wave equation, giving a description of the particle (for time $t$ , position $x$ ). If the state is square integrable, i.e.

$\int_{\mathbf R^n} |\psi_0(\mathbf x, t_0)|^2\, \mathrm{d\mathbf x} =: k^2 < \infty$

for some $t 0$ , then $ψ = ψ 0 / k$ is called the normalised wave function. Under the standard Copenhagen interpretation, the normalised wavefunction gives probability amplitudes for the position of the particle. Hence, at a given time $t 0$ , $ρ (x) = | ψ (x, t 0)| 2$ is the probability density function of the particle's position. Thus the probability that the particle is in the volume $V$ at $t 0$ is

$\mathrm \mathbf P(V)=\int_V \rho(\mathbf x)\, \mathrm{d\mathbf x} = \int_V |\psi(\mathbf x, t_0)|^2\, \mathrm{d\mathbf x}.$

Note that if any solution $ψ 0$ to the wave equation is normalisable at some time $t 0$ , then the $ψ$ defined above is always normalised, so that

$\rho_t(\mathbf x)=\left |\psi(\mathbf x, t)\right |^2 = \left|\frac{\psi_0(\mathbf x, t)}{k}\right|^2$

is always a probability density function for all $t$ . This is key to understanding the importance of this interpretation, because for a given initial $ψ (x, 0)$ , the Schrödinger equation fully determines subsequent wavefunction, and the above then gives the probable location of the particle at all subsequent times.

Non-normalisable states

Probability amplitudes which are not square integrable are usually interpreted as the limit of a series of functions which are square integrable. For example, the plane wave solution to the wave equation is not normalisable, so it is not possible to give a physical interpretation of it for a single particle. Instead, one way to interpret this solution is as an infinite stream of monochromatic (identical) particles, in this case the limit of the series giving the wavefunction for increasingly many particles. The definition of $P (V)$ given above is still valid, however since now many particles are involved, there could therefore be a high probability everywhere of finding a particle nearby.

Conservation relationship between probability amplitudes and probabilities

For more details on this topic and the proof, see probability current.

Intuitively, since a normalised wave function stays normalised while evolving according to the wave equation, there will be a relation between the change in the probability density of the particle's position and the change in the amplitude at these positions.

Define the probability current (or flux) $j$ as

$\mathbf{j} = {\hbar \over m} \cdot {1 \over {2 i}} \left( \psi ^{*} \nabla \psi - \psi \nabla \psi^{*} \right) = {\hbar \over m} \Im \left( \psi ^{*} \nabla \psi \right),$

measured in units of (probability)/(area × time).

Then the current satisfies the quantum continuity equation

$\nabla \cdot \mathbf{j} + { \partial \over \partial t} |\psi|^2 = 0.$

Discrete amplitudes

While the wave function describes the state of a system for the continuous variable position, there are also many discrete variables to which probabilities may also be attached, which in quantum mechanics are found from complex amplitudes.

Example: One-dimensional quantum tunnelling

For more details on this example, see finite potential barrier.

In the one-dimensional case of particles with energy less than $U > 0$ in the square potential

$V(x)=\begin{cases}U & |x|<a \\ 0 & \text{otherwise,}\end{cases}$

the steady-state solutions to the wave equation have the form (for some constants 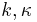$k, \kappa$ )

$\chi (x) = \left\{ \begin{array}{llrll} A\exp(ikx)+B\exp(-ikx) && x&<&-a \\ C\exp(\kappa x)+D\exp(-\kappa x) && |x|&\le&a \\ E\exp(ikx)+F\exp(-ikx) && x&>&a. \end{array} \right.$

The standard interpretation of this is as a stream of particles being fired at the step from the left (the direction of negative $x$ ): setting $A =1$ corresponds to firing particles singly; the terms containing $A$ , $C$ , and $E$ signify motion to the right, while $B$ , $D$ , and $F$ to the left. Under this beam interpretation, put $F = 0$ since no particles are coming from the right. By applying continuity of wave functions and their derivatives at the boundaries, it is hence possible to determine the constants above.

The conclusion is that the complex value $B$ is a probability amplitude, with a real interpretation in the problem. The corresponding probability $| B | 2$ describes the probability of a particle fired from the left being reflected by the potential barrier. Note that, very neatly, $| B | 2 +| E | 2 =1$ just as expected.

Notes

↑ Example taken from Raymond, David (2006-04-07). "Sense and Nonsense in Quantum Mechanics". http://physics.nmt.edu/~raymond/classes/ph13xbook/node71.html. Retrieved 2008-11-21.